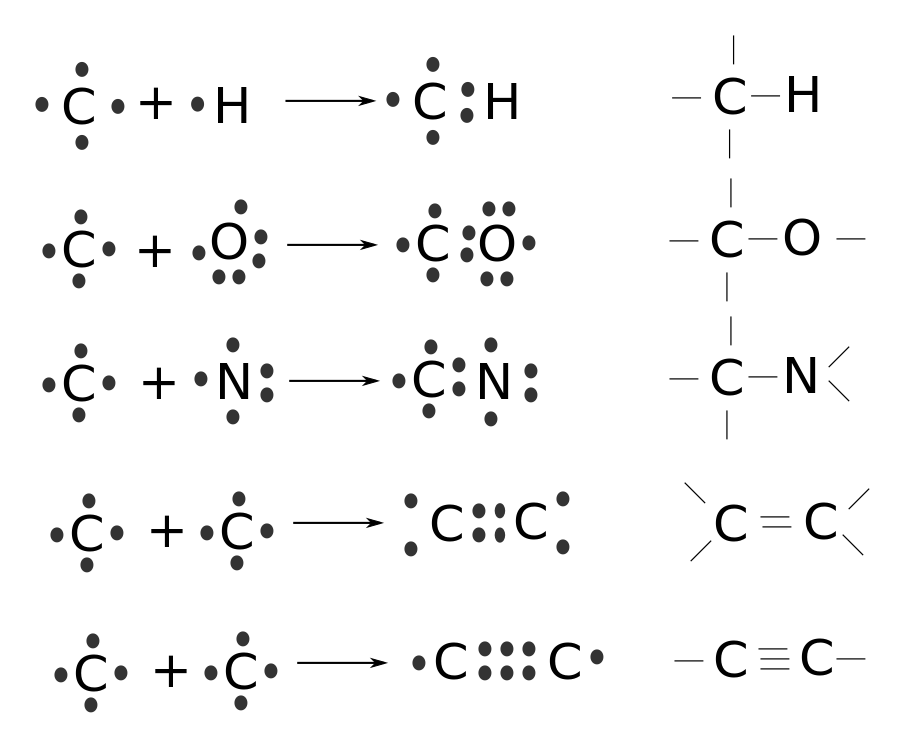Tag Archives: Atomic physics

Carbon

1

Now we are ready to understand how it is that carbon is such a versatile element. It is at the basis of all organic chemistry and, in particular, biochemistry. The functioning of all living things depends on water and on the versatility of the carbon atom.

We saw that the carbon atom’s electron-shell configuration was

12C: 1s22s22p2

so it has four electrons in its valence shell (n=2). That enables it to share its four electrons with four others from other atoms. The bonds tend to be equally spaced around the carbon atom in the form of a tetrahedron, like those little creamer packets you get in cheap restaurants. For instance, a carbon atom can bond with four hydrogens, sharing each of its four valence electrons with one hydrogen, so each hydrogen has two and the carbon has eight and everybody is happy. This is called methane and looks like this.

"Methane-2D-stereo" by SVG version by Patricia.fidi - Own work. Licensed under Public Domain via Wikimedia Commons.

Methane molecule, CH4 by Patricia.fidi via Wikimedia Commons.

You should see one of the lower-right-hand hydrogens as pointing up out of the page; the other, down into it. The angles between any two adjacent connecting lines (which of course are only imagined by us) are about 109.5°. Carbon’s versatility in binding is illustrated by the examples in this diagram.

Versatiliy of carbon bonding, after Lehninger.

The dots represent valence electrons and the right-hand column is another way of looking at the product in terms of bonds rather than electrons. Each line between atoms is a shared pair of electrons. Note the double and triple inter-carbon bonds in the last two examples. This large number of ways of bonding is the key to carbon’s versatility. In fact, compared to the huge number of such molecules possible, only a relatively small number of the same biomolecules occur in living organisms. This is the first example we see of nature using the same set of techniques or tools all over the biosphere.

Single bonds between carbons also exist, of course, and have the particular advantage that the carbons and whatever is bonded to them can rotate around the axis linking the two carbons. This is more important than one might think. It turns out that some proteins function differently in their left-handed and right-handed versions. Since rotation can change the shape of the molecule, this enables biomolecules with hundreds of atoms to take on specific shapes with definite mechanical or fluid properties. (We will see some of this in the biochemistry chapter.)

The importance of water is not just because we drink it. Let’s go look at that.

Atomic energy levels and chemical bonding

Reply

Atomic structure is the basis of chemistry. It is explained by Quantum Mechanics, which is part of physics. We will see that physics explains chemistry, which explains physiology, which at least start to explain neurobiology. It’s one thing that leads to another.

In QM, the properties of a system, that is, a given object or set of objects, such as an atom, are given by the solution to the Schrödinger equation for the system. For atoms, there are a set of solutions, corresponding to different energy states of the atoms. What follows may smack of numerology.

Consider the hydrogen atom, composed of one negatively-charged electron in orbit around a nucleus containing one positively-charged proton. (This is an experimental result.) Look out, the orbit is not a well-defined path around the nucleus like those animations you see in TV ads, but rather a cloud of probability which indicates the likelihood that the electron will be found at any given point in the cloud. This is due to the probabilistic character of QM and the Uncertainty Principle. The different solutions to the Schrödinger equation express the possible energy values of the atom. Each one is specified by a set of integer numbers called quantum numbers. In the case of the hydrogen atom, they are the following:

  1. The principal quantum number, designated by the symbol n, takes on integer values from 1 on up, but in practice only to 7. It indicates the shell, or level of the cloud, in which the electron is found. The values 1-7 are often indicated by the letters K, L, M…Q.

  2. The orbital quantum number, l, indicates a level within the shell which is called the subshell, It can take on values from 0 up to n-1. The values 0-3 are often referred to as s, p, d and f.1The notations s, p, d and f come from spectroscopy and are abbreviated forms of sharp, principal, diffuse and fundamental.

  3. The orbital magnetic quantum number, m, refers to the magnetic orientation of the electron. It can range from -l up through +l.

  4. The electron spin, ms, can take on only two values, ½ or -½.

So the only allowed values for the quantum numbers are

n = 1, 2, 3, …

l = 0…n-1 (for a given value of n)

m = -l…+l (for a given value of l)

because those are the ones for which the Schrödinger equation has solutions. It is actually quite simple.

The QM exclusion principle forbids two electrons to occupy the same state. So each set of values (n, l, m, ms) can correspond to only one electron. The result is illustrated in the following table.

n (shell)

l (subshell)

m (orbital)

Max no. electrons
1 0 0 2
2 0
1		 0
1		 2
6
3 0
1
2		 0
-1, 0, 1
-2. -1, 0, 1, 2		 2
6
10
4 0
1
2
3		 0
-1, 0, 1
-2, -1, 0, 1, 2
-3, -2, -1, 0, 1, 2, 3		 2
6
10
14

The fact that the quantum numbers do not vary continuously from, say, 0 to 0.001 and then 0.002 and on, but but jump from one integer value to another means that the energy of the electron in the electric field of the nucleus also takes on non-continuous values. These are called quantum states and are a feature, or if you prefer, a peculiarity, of QM.

The chemical properties of an atom depend only on the number of electrons. Unless the atom is chemically combined with another, the number of electrons is equal to the number of protons and is called the atomic number. All atoms except hydrogen have nuclei which also contain neutrons. As everyone knows, the number of neutrons can vary and atoms of an element with different numbers of neutrons are called isotopes. As we shall see, these are extraordinarily useful due to the fact that the properties of the element can vary from isotope to isotope.

In specifying which subshells are occupied by the electrons in an atom, one often uses the format

nl#

where l is specified as s, p, d or f and # is the number of electrons in the subshell. In its minimum energy state, called the ground state, the carbon atom (atomic number = 12, nucleus contains 6 protons and 6 neutrons) has the following electron configuration:

12C: 1s22s22p2

which indicates the maximum number of two electrons in shell 1, again in subshell s of shell 2 and the remaining two in subshell p of shell 2. Similarly, oxygen (atomic number = 16, 8 each of protons and neutrons) is

16O: 1s22s22p4

the meaning of which should now be clear.

What is interesting is that, for energetic reasons, each atom would like to have its outside subshell filled. If a few electrons are missing, it wants more; if most are missing, it might be willing to give up the rest in order to have an empty outside shell, referred to as the valence shell. (The number of electrons in this outer shell is called the valence.2Officially, the maximum number of univalent atoms (originally hydrogen or chlorine atoms) that may combine with an atom of the element under consideration, or with a fragment, or for which an atom of this element can be substituted.) For instance, hydrogen

1H: 1s1

wants two electrons or none in its 1s shell, so it could give up its electron or gain one. What happens is, two H atoms share their electrons to make a molecule of H2, so each has two electrons half the time. Better than nothing.3To continue the anthropomorphisms, this is a kind of solidarity in which humans are often lacking.

Since oxygen already has shell 2 half-filled, it would probably prefer to gain electrons to fill it. And carbon… but carbon is special and will be considered in a moment.

Look at sodium (Na, atomic number 11) and chlorine (Cl, atomic number 17):

Na: 1s22s22p63s1

Cl: 1s22s22p63s23p5

Sodium could happily give up that 3s electron and chlorine could use it to fill up its 3p valence shell. And this is what happens in table salt, NaCl. If you put salt in water, it separates (for reasons which will be discussed shortly) into charged ions, Na+ and Cl–, because chlorine is greedy and keeps that negative 3s electron it took away from sodium. This attraction for electrons is called electronegativity. This is very important in biochemical reactions in cells, as we shall see.

In brief, it turns out that elements with two, ten or eighteen electrons are particularly stable.

Chemistry is the study of chemical systems (atoms, molecules) and chemical bonding between such objects. In the case of NaCl, the sodium and chlorine have opposite electrical charge and the attractive electric force is what holds the molecule together. This is called ionic bonding. Sometimes, when atoms cannot decide which has more right to an electron, the electron is shared between them, as in H2, making both atoms relatively happy. Bonding based on shared electrons is called covalent bonding; it is a sort of consensus situation, if we may go on with the anthropomorphism.

Elements with the same number of electrons in their outer shells have similar chemical properties. So they are arranged in columns in that wonderful physical/chemical tool, the periodic table of the elements.

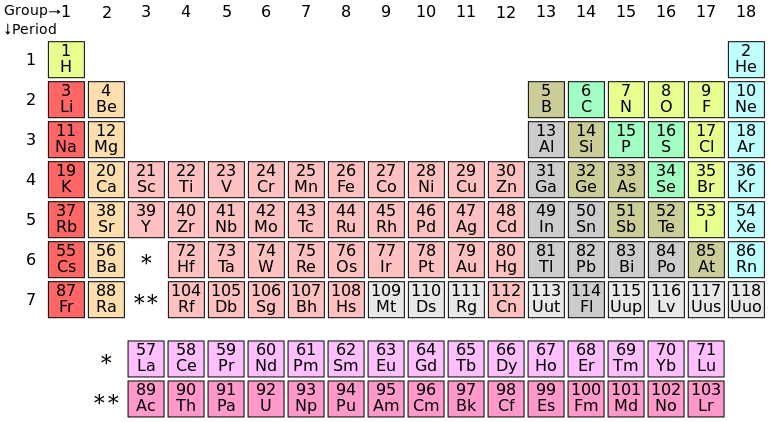
Periodic table of the elements

It is easy to see that each element in the first column is like hydrogen in having one electron in its valence shell.

H: 1s1

Li: 1s22s1

Na: 1s22s22p63s1

K: 1s22s22p63s23p64s1

… and so on.

The extra elements in the middle are rule-breakers. Instead of filling one subshell before moving on to the next, they start one, add a small number (often only one) of electrons to the next, then go back to finish filling the next-to-last.

Columns in the table are called groups; rows, periods.

The subshell configurations we have been giving are for the lowest energy state of the atom, called the ground state, in which subshells are filled from the “bottom” up (with some exceptions, as just mentioned). But if that hydrogen electron is struck by a photon, enough energy may be transferred from the photon to the 1s electron to push it into a higher-energy subshell. The atom is then said to be in an excited state. The electron may then re-descend spontaneously to the lower subshell, emitting a photon of energy equivalent to the difference in energy levels of the subshells. In QM, photons behave like waves whose energy is a function of their frequency, so the frequency – equivalently, the color – of the light emitted is characteristic of the difference in energy of the two subshells. Any atom’s subshells will therefore correspond to a given set of photon frequencies emitted and these are seen as colors, although not all these colors will be visible to a human eye. The set of frequencies constitute the spectrum of the atom and may be used to analyze the identity of a light source. In this way, we can identify the chemical components of light-emitting objects like distant stars.

There are two other types of bonding. We will consider hydrogen bonds very shortly in the discussion of water. The fourth form is due to the shifting electron density distribution around an atom. At times, this may form a temporary dipole even in a neutral atom. This may in turn induce a dipole in nearby atom in such a way that the two dipoles attract each other very weakly. This is London, or van der Waal’s, bonding.

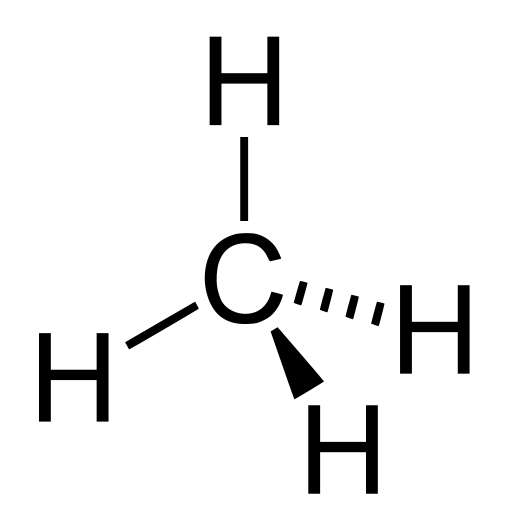
The functioning of all living things depends on water and on the versatility of the carbon atom. So let’s start with carbon.

Notes

Notes
↑1 The notations s, p, d and f come from spectroscopy and are abbreviated forms of sharp, principal, diffuse and fundamental.
↑2 Officially, the maximum number of univalent atoms (originally hydrogen or chlorine atoms) that may combine with an atom of the element under consideration, or with a fragment, or for which an atom of this element can be substituted.
↑3 To continue the anthropomorphisms, this is a kind of solidarity in which humans are often lacking.

What atomic physics and chemistry tell us

Reply

I am, reluctantly, a self-confessed carbon chauvinist. Carbon is abundant in the Cosmos. It makes marvelously complex molecules, good for life. I am also a water chauvinist. Water makes an ideal solvent system for organic chemistry to work in and stays liquid over a wide range of temperatures. But sometimes I wonder. Could my fondness for materials have something to do with the fact that I am made chiefly of them?

– Carl Sagan, Cosmos

The early stages of the universe and the lives of stars are the matter of physics and astronomy and their offspring, astrophysics and cosmology. By the time the first living things showed up on Earth, processes were occurring which require our knowing about the phenomena described by the science of chemistry. QM is the basis of atomic physics and that is the basis of chemistry, so we are ready for it.

To do even begin a comprehensive survey of chemistry is well beyond the scope of this document. We will illustrate its usefulness and some of its fruits by considering two subjects of great importance not only to Carl Sagan but to all of us – carbon and water.

In order to do that, it is necessary to know about several sujects:

Then we move on to consider, first, the past, starting almost 14 Gya.